There is an anecdote about Paul Erdos writing to Stan Ulam, who was at the time in a Los Alamos hospital recovering from brain surgery. The letter went something like this: 'Dear Stan, I hope you are well. Let n be a prime number...' I'm afraid, dear David, my birthday wishes will have the same sentiment. Happy birthday. Now, remember those discussions we had about Popper and his views on democracy? You explained to me the counterintuitive point that true democracy is not so much about choosing leaders; it's really about facilitating the removal of bad leaders. This realization struck me at 3 am while I was chewing a slice of mince pie in your kitchen. It led us from Karl Popper to electoral systems, and we had a lot of fun examining Kenneth Arrow's no-go theorems and the Balinsky and Young argument, which shows the impossibility of designing the perfect apportionment system. I have very fond memories of these discussions, and I was delighted when I recently stumbled upon some old notes on the subject. One simple geometric illustration caught my attention, demonstrating that any apportionment system can go wrong.
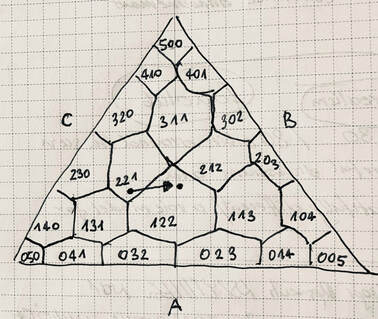
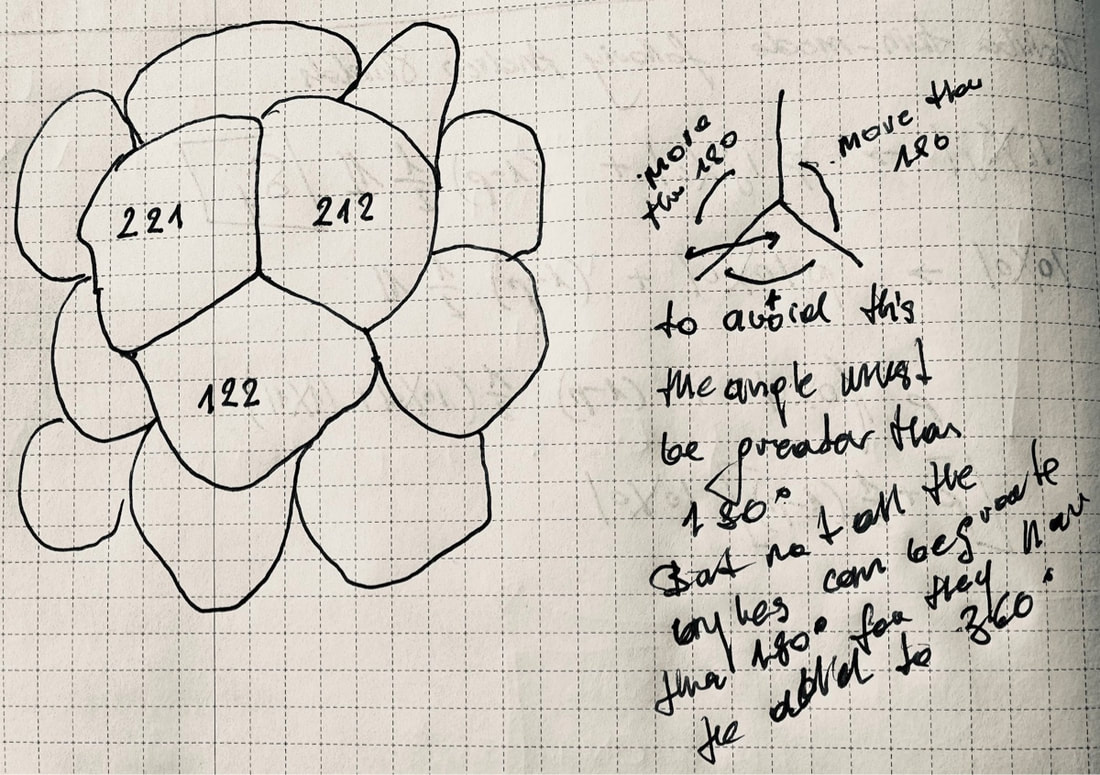
Let's imagine three parties—A, B, and C—competing for 5 seats in a house. To visualise the apportionment problem, I draw an equilateral triangle with a height of 100 units and label its sides as A, B, and C, respectively. The sum of the distances from any point within the triangle to sides A, B, and C will always be 100 units. Hence, any point inside the triangle represents the percentage of votes for each of the three parties. We can partition the triangle into regions labelled by triplets (a, b, c) representing the number of seats allocated to parties A, B, and C, respectively. Different partitions correspond to different allocation methods. It is reasonable to require that the whole number a can only increase as the distance of the point from side A increases, and the same must be true for whole numbers b and c. Here, I have sketched one such partition and indicated, with an arrow, that the partition (and hence the corresponding apportionment system) does not satisfy this condition. Party A gained votes but lost one seat. In fact, this holds true for any partition. I have sketched the second picture to illustrate this, but I'll leave it to you to figure out the details.
PS Anyway, I am not Erdos, so congratulations on completing 70 orbits around the Sun, and in this context, the phrase "many happy returns" takes on even greater significance!
PS Anyway, I am not Erdos, so congratulations on completing 70 orbits around the Sun, and in this context, the phrase "many happy returns" takes on even greater significance!